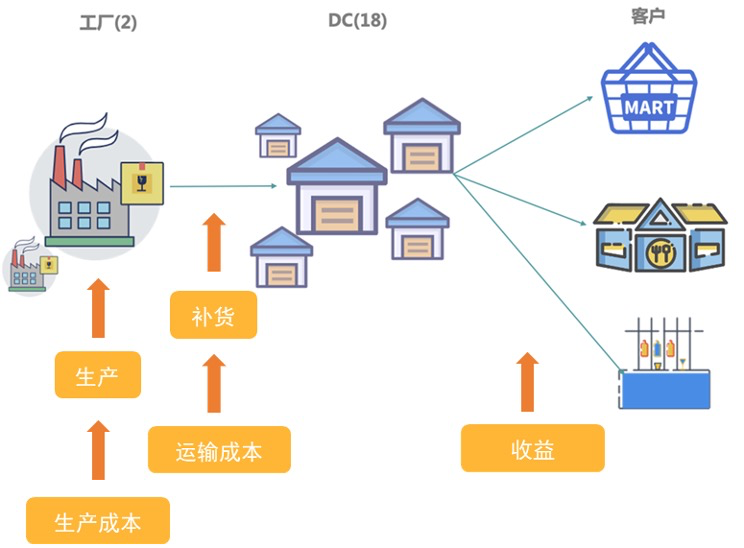
饮料企业多工厂生产与补货优化
本文基于某饮料企业的工厂、仓库与商品相关的历史信息,结合随机模拟的售价与成本数据,构建了多工厂、多仓库的生产与补货优化模型。
数值试验表明,本文构建的优化后的生产与补货模型能够比基线模型(简单基于历史销量而固定生产量)多获得约 500 万元的利润,且在补货行为上更具优势。对工厂和仓库容量的灵敏度分析表明,工厂 2 和 DC4、5、7、14 多具有当前容量较小、运输成本低、历史销量高等特点,对它们进行扩容能够取得显著的回报增益。对整托约束的松弛表明,整托运输虽以节省运输成本为目的,但实际却可能造成运输资源的浪费,而考虑适当放松整托约束有潜力能够提高约 100 万元的利润。