跳转至

Transformer 中的 Positional Encoding Layer

在 Transformer 的模型结构中，Positional Encoding Layer 是将输入文本进行位置编码，使得模型知道每个词在文本中的绝对位置和相对位置。有时，当一个词的位置发生变化后，语义会发生巨大的变化，因此 Positional Encoding Layer 是至关重要的。

Transformer 原始论文中只给出了关键的编码公式，而我第一次看到这个公式时觉得晦涩难懂。深度学习课程的老师在课上讲解了之后，我还是不太明白。

\[ \begin{aligned} P E(p o s, 2 i+1)&=\cos \left(\frac{p o s}{10000^{2 i / d m o d e l}}\right) \\ P E(p o s, 2 i)&=\sin \left(\frac{p o s}{10000^{2 i / d m o d e l}}\right) \end{aligned} \]

终于，我找到了写得非常好的资料。作者从最简单的绝对位置编码（也就是将第一个位置编码为 1，第二个位置编码为 2，以此类推。这当然是最容易想到的方法。）开始介绍，一步一步引导我们为什么要用上面的公式。

image-20230430211441325

个人理解

Encoding 本质上是用尽量少的空间去表示一个大的内容。这让我联想到两个例子：

  1. 变速自行车通过两个变速器对速度档位进行调节。以我的自行车为例，左边把手装的是大变速器，一共有 \(3\) 个档位；右边把手装的是小变速器，一共有 \(7\) 个档位。这样，我只需要调节 \(2\) 个变速器，就可以获得 \(3\times7\) 个不同的档位。
  2. 显微镜的粗准焦螺旋和细准焦螺旋。前者能够使显微镜的镜筒大幅度位移，后者则能够使镜筒小幅度的位移。两个配合使用，就能够只做少量旋转达到大幅且精准的调节。

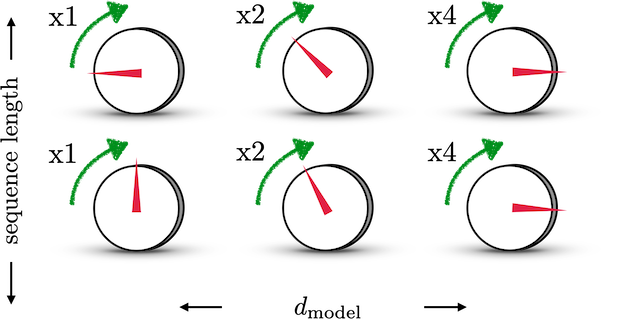
以下是 https://machinelearningmastery.com/a-gentle-introduction-to-positional-encoding-in-transformer-models-part-1/ 给出的直观理解：将位置向量的每个位置想象成一个拨号器。对最左侧的拨号器，每拨一格，其值加 1；最右侧的拨号器，每拨一格，其值加 4。这样就能够实现：只拨动很少的格子，也能表示一个很大的数。

img

如何表示相对位置

这样的 Positional Encoding 可以蕴含两个文本的相对位置信息，因为 \(\cos (\theta+\phi)\) 和 \(\sin (\theta+\phi)\) 可以通过 \(\cos (\theta)\) 和 \(\sin (\theta)\) 结合 \(\phi\) 来得到。

\[ \left(\begin{array}{c} \cos (\theta+\phi) \\ \sin (\theta+\phi) \end{array}\right)=\left(\begin{array}{cc} \cos \phi & -\sin \phi \\ \sin \phi & \cos \phi \end{array}\right)\left(\begin{array}{c} \cos \theta \\ \sin \theta \end{array}\right) \]

image-20230601122415731

image-20230601122348816

image-20230601122255867

代码实现

Python
import numpy as np
import matplotlib.pyplot as plt
Python
def getPositionEncoding(seq_len, d, n=10000):
    P = np.zeros((seq_len, d))
    for k in range(seq_len):
        for i in np.arange(int(d / 2)):
            denominator = np.power(n, 2 * i / d)
            P[k, 2 * i] = np.sin(k / denominator)
            P[k, 2 * i + 1] = np.cos(k / denominator)
    return P


P = getPositionEncoding(seq_len=4, d=4, n=100)
print(P)
Text Only
[[ 0.          1.          0.          1.        ]
 [ 0.84147098  0.54030231  0.09983342  0.99500417]
 [ 0.90929743 -0.41614684  0.19866933  0.98006658]
 [ 0.14112001 -0.9899925   0.29552021  0.95533649]]

img

Python
P = getPositionEncoding(seq_len=100, d=256, n=10000)
cax = plt.matshow(P)
plt.gcf().colorbar(cax)
plt.show()

image-20230430211441325

看图找规律

  1. 只看第一行，也就是第 0 个词，它的颜色是黄绿交替的，也就是 0、1 交替的。这是因为当 pos=0 时，\(P E(p o s, 2 i+1)\) 都等于 \(1\)，\(P E(p o s, 2 i)\) 都等于 \(0\)。
  2. 越靠右边，位置编码的数值在纵向的变动越慢。这是因为 \(\sin\) 函数中 \(pos\) 的系数是 \(\frac{1}{10000^{2 i / d m o d e l}}\)，\(i\) 越来越大，因此这个系数越来越小，导致 \(\sin\) 的频率越来越低了，要隔很久才能重新开始一个周期。 我们可以将右侧编码理解为粗准焦螺旋（大范围地调节），左侧编码理解为细准焦螺旋（小范围地调节）。
  3. 两个相邻的行，它们的颜色样式比较相近，这表示它们的位置比较接近。

评论