使用 Gradient Boost Decision Tree 进行回归预测

使用 GBDT 进行回归预测，并与决策树进行对比。

GBDT 的损失值随迭代次数的变化

学到了什么

• GBDT 的参数中，learning_rate很重要，在本例中设为\(0.01\)比较合适。若设为\(0.1\)则很容易过拟合。

• 画图中，坐标轴显示百分比，可以用

Python

from matplotlib.ticker import PercentFormatter

# ylabel 以百分数的形式显示
ax.yaxis.set_major_formatter(PercentFormatter(xmax=1.0, decimals=0))

• xmax=1.0代表原始数据是 0.1、0.2 这种，想要显示为 10%、20%。如果原始数据是 10、20，想要显示为 10%、20%，则需要设置xmax为 100。
• decimals是百分比中保留几位小数。

官方文档

Python

# 导入包
import pandas as pd
import numpy as np
from tqdm.notebook import tqdm
import matplotlib.pyplot as plt
from matplotlib.ticker import PercentFormatter

plt.rcParams["font.sans-serif"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = False
from scipy.stats import pearsonr
from sklearn.preprocessing import MinMaxScaler
from sklearn.feature_selection import VarianceThreshold
from sklearn.feature_extraction import FeatureHasher
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import GradientBoostingRegressor
from sklearn import metrics

读取数据

Python

# 读取数据
train = pd.read_excel("HousePrices.xlsx", sheet_name="train")
test = pd.read_excel("HousePrices.xlsx", sheet_name="test", header=None)
test.columns = train.columns
x_train = train.drop(["SalePrice"], axis=1)
y_train = train["SalePrice"]
x_test = test.drop(["SalePrice"], axis=1)
y_test = test["SalePrice"]

处理缺失值

查看缺失值

Python

column_with_null = x_train[x_train.columns[x_train.isna().any()]].isnull().sum()
print(column_with_null)

Text Only

LotFrontage      192
Alley           1031
MasVnrType         6
MasVnrArea         6
BsmtQual          31
BsmtCond          31
BsmtExposure      32
BsmtFinType1      31
BsmtFinType2      32
FireplaceQu      524
GarageType        61
GarageYrBlt       61
GarageFinish      61
GarageQual        61
GarageCond        61
PoolQC          1098
Fence            892
MiscFeature     1054
dtype: int64

适合用均值填充的列：

Python

# 适合用均值填充的列
fillna_with_mean = ["LotFrontage", "MasVnrArea", "GarageYrBlt"]

for col in fillna_with_mean:
    x_train[col].fillna(x_train[col].mean(), inplace=True)
    x_test[col].fillna(x_test[col].mean(), inplace=True)

适合用'None'填充的列：

Python

# 适合用 None 填充的列
fillna_with_none = list(set(x_train.columns) - set(fillna_with_mean))

for col in fillna_with_none:
    x_train[col].fillna("None", inplace=True)
    x_test[col].fillna("None", inplace=True)

特征编码

大部分特征均为文本型，且包含多个无序的文本值。可以将这些文本值通过哈希编码转换为数值型，以便于后续的建模。

使用n_features参数控制哈希编码的维度，这里将维度设为 2，即将文本值转换为二维的数值型特征。数据集中的特征最多有 10 余个唯一值，因此二维哈希值足以对数据集中的特征进行编码。

Python

# 文本特征的列
text_features = list(x_train.columns[x_train.dtypes == "object"])

# # 哈希编码器
for col in text_features:
    hash_encoder = FeatureHasher(n_features=2, input_type="string")
    # 对原始特征进行编码，得到哈希值数组
    x_train_col_hashed = hash_encoder.fit_transform(x_train[col]).toarray()
    x_test_col_hashed = hash_encoder.transform(x_test[col]).toarray()
    # 转换为数据框
    x_train_col_hashed = pd.DataFrame(
        x_train_col_hashed, columns=[col + "_" + str(i) for i in range(1, 2 + 1)]
    )
    x_test_col_hashed = pd.DataFrame(
        x_test_col_hashed, columns=[col + "_" + str(i) for i in range(1, 2 + 1)]
    )
    # 删除原有的文本特征
    x_train.drop(col, axis=1, inplace=True)
    x_test.drop(col, axis=1, inplace=True)
    # 将哈希编码后的特征添加到数据集中
    x_train = pd.concat([x_train, x_train_col_hashed], axis=1)
    x_test = pd.concat([x_test, x_test_col_hashed], axis=1)

特征选择

移除低方差特征

Python

# 删除 id 列
x_train.drop(["Id"], axis=1, inplace=True)
x_test.drop(["Id"], axis=1, inplace=True)
# 将特征进行最小最大归一化
scaler = MinMaxScaler()
x_train = pd.DataFrame(
    scaler.fit_transform(x_train), index=x_train.index, columns=x_train.columns
)
x_test = pd.DataFrame(
    scaler.transform(x_test), index=x_test.index, columns=x_test.columns
)
# 移除低方差（归一化后方差小于 0.005）特征
selector = VarianceThreshold(threshold=0.005)
selector.fit(x_train)
# 打印因为低方差被移除的特征
print("因为低方差被移除特征：", x_train.columns[~selector.get_support()])
x_train = x_train.loc[:, selector.get_support()]
x_test = x_test.loc[:, selector.get_support()]

Text Only

因为低方差被移除特征： Index(['LotArea', '3SsnPorch', 'PoolArea', 'MiscVal', 'Street_1', 'Street_2',
       'Utilities_1', 'Utilities_2', 'Condition2_1', 'Condition2_2',
       'RoofMatl_1', 'Foundation_2', 'Heating_2', 'CentralAir_1',
       'CentralAir_2', 'PavedDrive_1', 'PavedDrive_2', 'PoolQC_1', 'PoolQC_2',
       'MiscFeature_1', 'MiscFeature_2'],
      dtype='object')

移除高相关特征中方差较低的那一个

由于特征变量众多，这里不再绘制相关系数热力图。

Python

corr = x_train.corr()
# 打印相关性绝对值大于 0.8 的特征
corr = corr.abs()
corr = corr.where(np.triu(np.ones(corr.shape), k=1).astype(bool))
corr = corr.stack()
corr = corr[corr > 0.8]
print("相关性绝对值大于 0.8 的特征：", [i for i in corr.index])
# 从数据集中移除相关性绝对值大于 0.8 的特征中方差较小的特征
feature_to_remove = []
corr = corr.reset_index()
corr.columns = ["feature1", "feature2", "corr"]
for row in corr.itertuples():
    if x_train[row.feature1].var() < x_train[row.feature2].var():
        feature_to_remove.append(row.feature1)
    else:
        feature_to_remove.append(row.feature2)
feature_to_remove = list(set(feature_to_remove))
print("相关性绝对值大于 0.8 的特征中方差较小的特征：", feature_to_remove)
x_train.drop(feature_to_remove, axis=1, inplace=True)
x_test.drop(feature_to_remove, axis=1, inplace=True)

Text Only

相关性绝对值大于0.8的特征： [('TotalBsmtSF', '1stFlrSF'), ('GrLivArea', 'TotRmsAbvGrd'), ('Fireplaces', 'FireplaceQu_1'), ('GarageCars', 'GarageArea'), ('LotShape_1', 'LotShape_2'), ('LandContour_1', 'LandContour_2'), ('LotConfig_1', 'LotConfig_2'), ('RoofStyle_1', 'RoofStyle_2'), ('Exterior1st_1', 'Exterior2nd_1'), ('Exterior1st_2', 'Exterior2nd_2'), ('ExterQual_1', 'ExterQual_2'), ('ExterCond_1', 'ExterCond_2'), ('BsmtQual_1', 'BsmtQual_2'), ('BsmtCond_1', 'BsmtCond_2'), ('HeatingQC_1', 'HeatingQC_2'), ('Electrical_1', 'Electrical_2'), ('KitchenQual_1', 'KitchenQual_2'), ('GarageType_1', 'GarageFinish_1'), ('GarageType_1', 'GarageQual_1'), ('GarageType_1', 'GarageCond_1'), ('GarageType_1', 'GarageCond_2'), ('GarageFinish_1', 'GarageQual_1'), ('GarageFinish_1', 'GarageCond_1'), ('GarageFinish_1', 'GarageCond_2'), ('GarageQual_1', 'GarageQual_2'), ('GarageQual_1', 'GarageCond_1'), ('GarageQual_1', 'GarageCond_2'), ('GarageQual_2', 'GarageCond_1'), ('GarageCond_1', 'GarageCond_2')]
相关性绝对值大于0.8的特征中方差较小的特征： ['BsmtCond_1', 'HeatingQC_1', 'LandContour_2', 'BsmtQual_1', 'RoofStyle_2', 'Exterior2nd_2', 'Electrical_2', 'GrLivArea', 'GarageCond_2', 'ExterQual_2', 'GarageQual_2', 'KitchenQual_2', 'ExterCond_2', 'GarageArea', 'GarageType_1', 'LotConfig_1', 'GarageFinish_1', '1stFlrSF', 'Fireplaces', 'GarageCond_1', 'Exterior1st_1', 'LotShape_1']

移除与标签相关性较低的特征

Python

# 移除与标签相关性绝对值小于 0.02 的特征
feature_to_remove = []
for i in x_train.columns:
    pearson_corr = pearsonr(x_train[i], y_train)[0]
    if abs(pearson_corr) < 0.02:
        feature_to_remove.append(i)
print("与标签相关性绝对值小于 0.02 的特征：", feature_to_remove)
x_train.drop(feature_to_remove, axis=1, inplace=True)
x_test.drop(feature_to_remove, axis=1, inplace=True)

Text Only

与标签相关性绝对值小于0.02的特征： ['BsmtFinSF2', 'LandContour_1', 'Exterior2nd_1', 'Functional_2']

最终选择的特征

Python

# 打印最终选择的特征
print("最终选择的特征", x_train.columns.values)

Text Only

最终选择的特征 ['MSSubClass' 'LotFrontage' 'OverallQual' 'OverallCond' 'YearBuilt'
 'YearRemodAdd' 'MasVnrArea' 'BsmtFinSF1' 'BsmtUnfSF' 'TotalBsmtSF'
 '2ndFlrSF' 'LowQualFinSF' 'BsmtFullBath' 'BsmtHalfBath' 'FullBath'
 'HalfBath' 'BedroomAbvGr' 'KitchenAbvGr' 'TotRmsAbvGrd' 'GarageYrBlt'
 'GarageCars' 'WoodDeckSF' 'OpenPorchSF' 'EnclosedPorch' 'ScreenPorch'
 'MoSold' 'YrSold' 'MSZoning_1' 'MSZoning_2' 'Alley_1' 'Alley_2'
 'LotShape_2' 'LotConfig_2' 'LandSlope_1' 'LandSlope_2' 'Neighborhood_1'
 'Neighborhood_2' 'Condition1_1' 'Condition1_2' 'BldgType_1' 'BldgType_2'
 'HouseStyle_1' 'HouseStyle_2' 'RoofStyle_1' 'RoofMatl_2' 'Exterior1st_2'
 'MasVnrType_1' 'MasVnrType_2' 'ExterQual_1' 'ExterCond_1' 'Foundation_1'
 'BsmtQual_2' 'BsmtCond_2' 'BsmtExposure_1' 'BsmtExposure_2'
 'BsmtFinType1_1' 'BsmtFinType1_2' 'BsmtFinType2_1' 'BsmtFinType2_2'
 'Heating_1' 'HeatingQC_2' 'Electrical_1' 'KitchenQual_1' 'Functional_1'
 'FireplaceQu_1' 'FireplaceQu_2' 'GarageType_2' 'GarageFinish_2'
 'GarageQual_1' 'Fence_1' 'Fence_2' 'SaleType_1' 'SaleType_2'
 'SaleCondition_1' 'SaleCondition_2']

构建 Gradient Boost Decision Tree 回归器

Python

GBDT_reg = GradientBoostingRegressor(
    n_estimators=500,
    learning_rate=0.1,
    max_depth=3,
    random_state=0,
    loss="squared_error",
)
GBDT_reg.fit(x_train, y_train)
y_pred = GBDT_reg.predict(x_test)

模型评价

Python

# 模型评价
def evaluate(y_test, y_pred):
    print("均方误差：", metrics.mean_squared_error(y_test, y_pred))
    print(
        "平均相对误差：{:.2%}".format(metrics.mean_absolute_percentage_error(y_test, y_pred))
    )


evaluate(y_test, y_pred)

Text Only

均方误差： 720867681.3136929
平均相对误差：10.28%

参数调优：迭代次数

Python

n_estimators_range = range(100, 2001, 50)
mean_squared_error_list = []
mean_absolute_percentage_error_list = []
for n_estimators in tqdm(n_estimators_range):
    GBDT_reg = GradientBoostingRegressor(
        n_estimators=n_estimators,
        learning_rate=0.01,
        max_depth=5,
        random_state=0,
        loss="squared_error",
    )
    GBDT_reg.fit(x_train, y_train)
    y_pred = GBDT_reg.predict(x_test)
    mean_squared_error_list.append(metrics.mean_squared_error(y_test, y_pred))
    mean_absolute_percentage_error_list.append(
        metrics.mean_absolute_percentage_error(y_test, y_pred)
    )

Text Only

  0%|          | 0/39 [00:00<?, ?it/s]

Python

# 绘制迭代次数与测试误差的关系图
fig = plt.figure(figsize=(9, 6), dpi=200)
ax1 = fig.add_subplot(111)
ax1.plot(
    n_estimators_range,
    mean_squared_error_list,
    "r-o",
    markerfacecolor="none",
    label="均方误差（左轴）",
)
ax1.set_xlabel("Gradient Boost Decision Tree 迭代次数")
ax1.set_ylabel("均方误差")
ax2 = ax1.twinx()
ax2.plot(
    n_estimators_range,
    mean_absolute_percentage_error_list,
    "b-o",
    markerfacecolor="none",
    label="平均相对误差（右轴）",
)
ax2.set_ylabel("平均相对误差", rotation=270, labelpad=15)
# ylabel 以百分数的形式显示
ax2.yaxis.set_major_formatter(PercentFormatter(1.0, decimals=0))
fig.legend(loc=1, bbox_to_anchor=(0.88, 0.85))
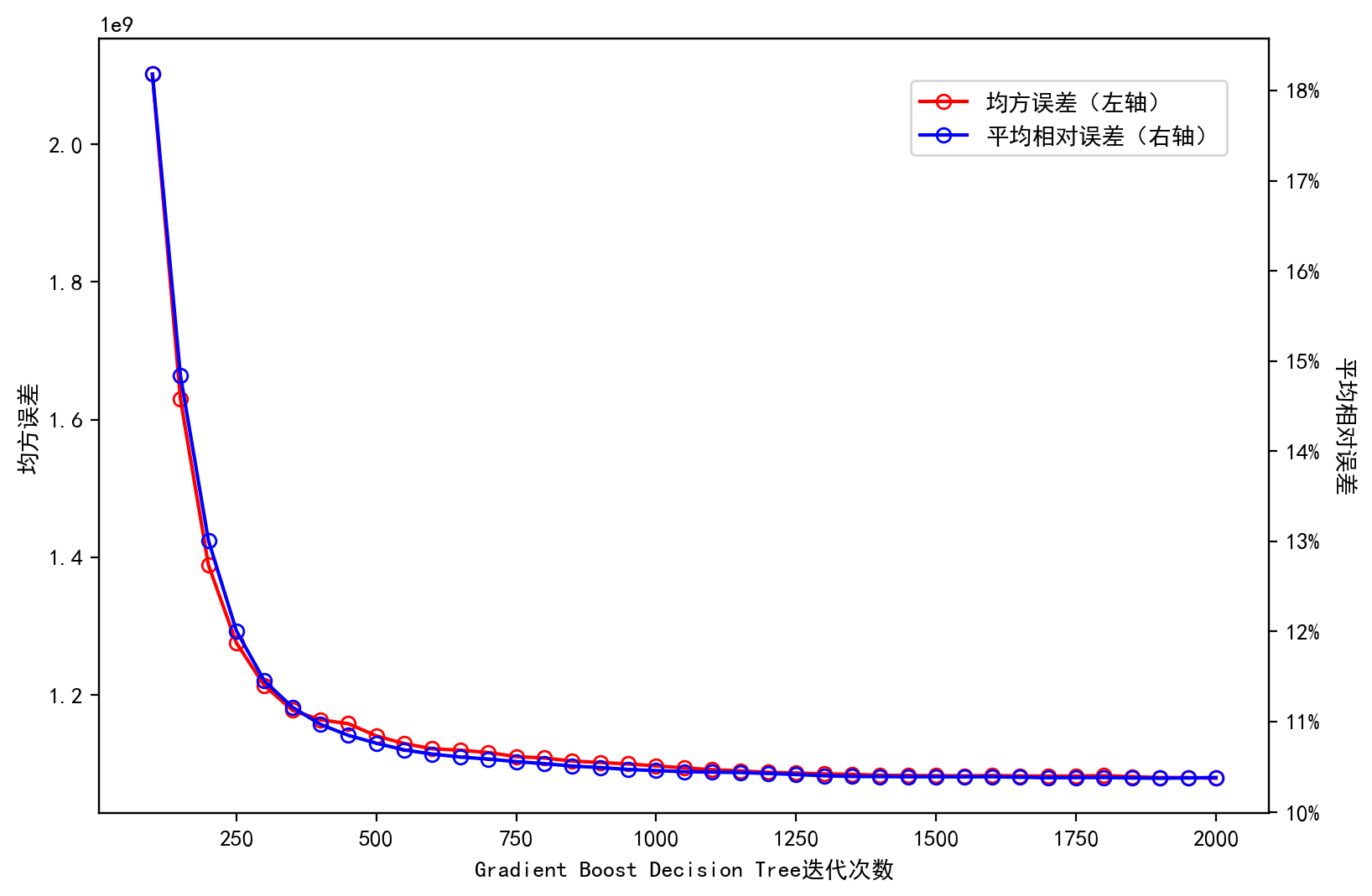
plt.show()

​

可以看到，当迭代次数增加到 1000 左右时，模型在测试集上的平均相对误差基本稳定在 10.3% 左右。因此，可以将最好的迭代次数设为 1000。

与决策树做对比

Python

max_depth_range = range(2, 21)
mean_squared_error_list_decision_tree = []
mean_absolute_percentage_error_list_decision_tree = []
for max_depth in tqdm(max_depth_range):
    decision_tree_reg = DecisionTreeRegressor(max_depth=max_depth)
    decision_tree_reg.fit(x_train, y_train)
    y_pred = decision_tree_reg.predict(x_test)
    mean_squared_error_list_decision_tree.append(
        metrics.mean_squared_error(y_test, y_pred)
    )
    mean_absolute_percentage_error_list_decision_tree.append(
        metrics.mean_absolute_percentage_error(y_test, y_pred)
    )

Text Only

  0%|          | 0/19 [00:00<?, ?it/s]

Python

# 绘制决策树最大树深度与测试误差的关系图
fig = plt.figure(figsize=(9, 6), dpi=200)
ax1 = fig.add_subplot(111)
ax1.plot(
    max_depth_range,
    mean_squared_error_list_decision_tree,
    "r-o",
    markerfacecolor="none",
    label="均方误差（左轴）",
)
ax1.set_xticks(max_depth_range)
ax1.set_xlabel("决策树最大树深度")
ax1.set_ylabel("均方误差")
ax2 = ax1.twinx()
ax2.plot(
    max_depth_range,
    mean_absolute_percentage_error_list_decision_tree,
    "b-o",
    markerfacecolor="none",
    label="平均相对误差（右轴）",
)
ax2.set_ylabel("平均相对误差", rotation=270, labelpad=15)
# y 轴百分比
ax2.yaxis.set_major_formatter(PercentFormatter(1.0, decimals=0))
fig.legend(loc=1, bbox_to_anchor=(0.88, 0.85))
plt.show()

​

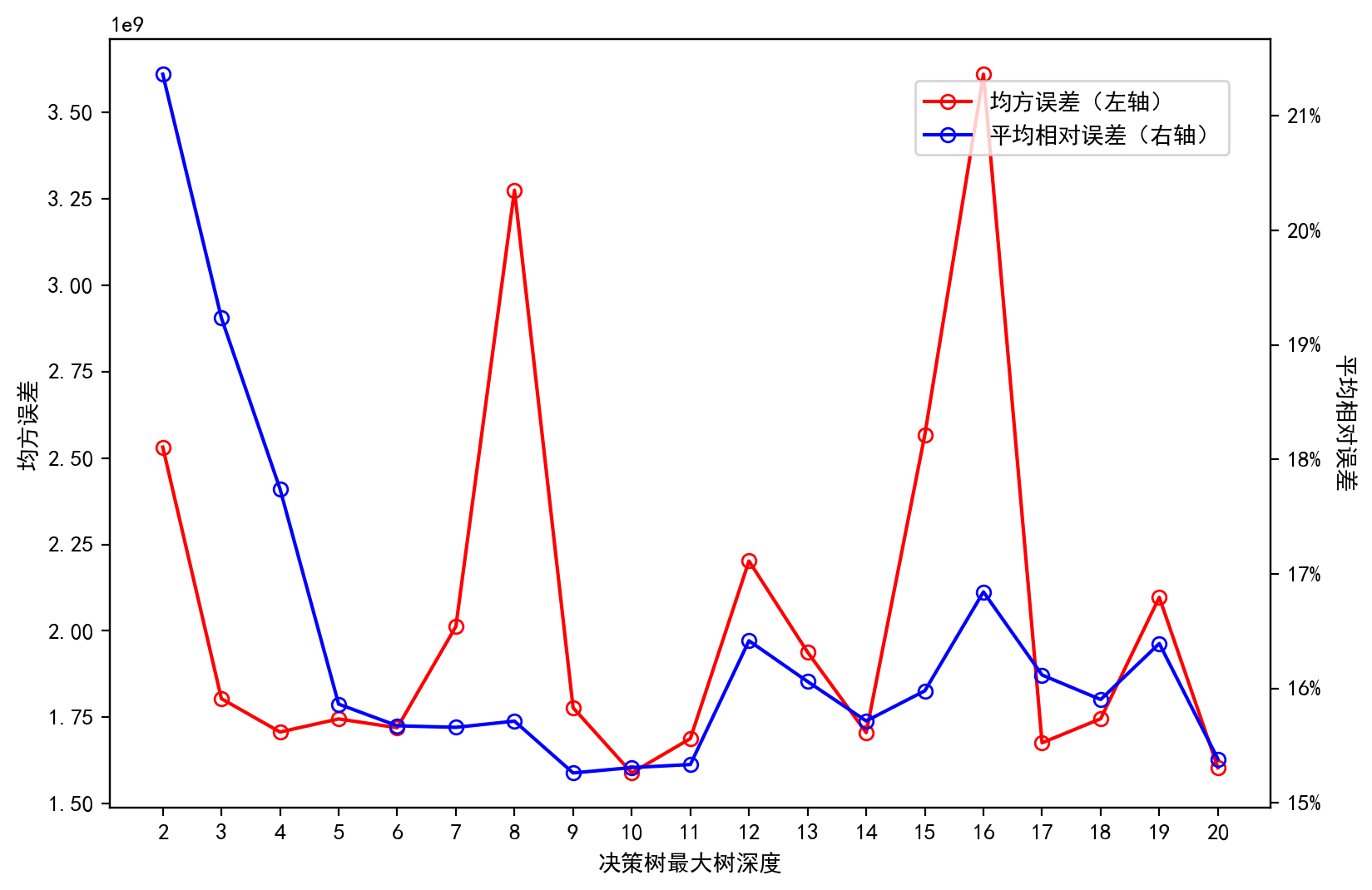
可以看到，决策树中最大数深度大于 6 时，模型开始出现过拟合现象。最优的最大树深度为 5，此时模型在测试集上的平均相对误差约为 15%，高于 Gradient Boost Decision Tree 模型的 10.3%。

评论