L1、L2 正则化与贝叶斯先验
从贝叶斯统计的视角看,L1 正则化的 Lasso 回归和 L2 正则化的岭回归,分别相当于参数具有拉普拉斯先验和高斯先验。
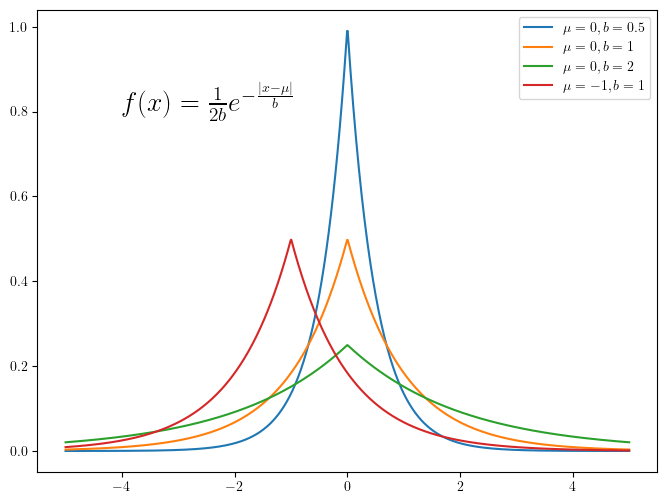
拉普拉斯分布的概率密度函数图像
零信息先验等价于最小二乘法
假设需要从一些样本点\((\boldsymbol{X}_1,Y_1)···(\boldsymbol{X}_n,Y_n)\)中来估计参数\(\boldsymbol{\boldsymbol{\beta}}\),假设输出\(Y_i\)与输入\(\boldsymbol{X}_i\)之间线性相关,并且受噪声\(\epsilon\)影响:
\[
Y_i=\boldsymbol{X}_i ^\mathsf{T} \boldsymbol{\beta} +\epsilon_i
\]
其中,\(\epsilon_i \overset{\mathrm{iid}}{\sim} N(0,\sigma^2)\)。
对样本\((\boldsymbol{X}_i,Y_i)\),基于\(\boldsymbol{X}_i\)得到\(Y_i\)的过程,可以认为是产生随机变量\(Y_i\sim N(\boldsymbol{X}_i ^\mathsf{T} \boldsymbol{\boldsymbol{\beta}},\sigma^2)\)的过程。
则似然函数为
\[
P(Y_i|\boldsymbol{X}_i,\boldsymbol{\beta})=\frac{1} {\sigma\sqrt{2\pi}}e^{-\frac{\lVert \boldsymbol{X}_i ^\mathsf{T} \boldsymbol{\beta}-Y_i\rVert^2} {2\sigma^2}}
\]
对所有样本,假设每个样本之间是相互独立的,则基于所有样本的似然函数为
\[
P(\boldsymbol{Y}|\boldsymbol{X},\boldsymbol{\beta})=\prod_i\frac{1} {\sigma\sqrt{2\pi}}e^{-\frac{\lVert \boldsymbol{X}_i ^\mathsf{T} \boldsymbol{\beta}-Y_i\rVert^2} {2\sigma^2}}
\]
最大化似然函数,求得最优的\(\boldsymbol{\beta}\),即
\[
\begin{aligned}
\boldsymbol{\beta}^* &= \underset{\boldsymbol{\beta}}{\operatorname{argmax}}(\prod _i\frac{1} {\sigma\sqrt{2\pi}}e^{-\frac{\lVert \boldsymbol{X}_i ^\mathsf{T} \boldsymbol{\beta}-Y_i\rVert^2} {2\sigma^2}}) \\\
&= \underset{\boldsymbol{\beta}}{\operatorname{argmax}}(-\sum _i\ln(\sigma \sqrt{2\pi}) -\frac{1} {2\sigma^2}\sum _i\lVert \boldsymbol{X}_i ^\mathsf{T} \boldsymbol{\beta}-Y_i\rVert^2)\\\
&= \underset{\boldsymbol{\beta}}{\operatorname{argmin}}(\sum _i \lVert \boldsymbol{X}_i ^\mathsf{T} \boldsymbol{\beta}-Y_i\rVert^2)
\end{aligned}
\]
在不加任何先验(或者零信息先验,即\(\boldsymbol{\beta}\)的先验分布是均匀分布)时,这就是最小二乘法。
拉普拉斯先验等价于带有 L1 正则项的 Lasso 回归
若对\(\boldsymbol{\boldsymbol{\beta}}\)的每个分量\(\beta_j, j=1,2,\cdots,p\)(\(p\)为\(\boldsymbol{X}\)的维数)施加拉普拉斯先验
\[
P(\beta_j)=f(\beta_j|\mu, b) = \frac{1}{2b} \exp(-\frac{|\beta_j-\mu|}{b})
\]
拉普拉斯分布的概率密度函数图像
Python# 绘制拉普拉斯分布的概率密度函数
def laplace(mu, b, x):
return 1 / (2 * b) * np.exp(-abs(x - mu) / b)
x = np.linspace(-5, 5, 1000)
plt.rcParams["text.usetex"] = True
fig = plt.figure(figsize=(8, 6))
mu = 0
for b in [0.5, 1, 2]:
plt.plot(x, laplace(mu, b, x), label=r"$\mu={}, b={}$".format(mu, b))
mu = -1
b = 1
plt.plot(x, laplace(mu, b, x), label=r"$\mu={}, b={}$".format(mu, b))
# 在图中添加文字,显示概率密度函数
plt.text(-4, 0.8, r"$f(x)=\frac{1}{2b}e^{-\frac{|x-\mu|}{b}}$", fontsize=20)
plt.legend()
plt.show()

则\(\boldsymbol{\beta}\)的后验分布为
\[
P(\boldsymbol{\beta} | \boldsymbol{X},\boldsymbol{Y}) \propto P(\boldsymbol{Y}|\boldsymbol{X},\boldsymbol{\beta}) P(\boldsymbol{\beta})
\]
最大化后验分布,求得最优的\(\boldsymbol{\beta}\),即
\[
\begin{aligned}
\boldsymbol {\beta} ^* &= \underset{\boldsymbol{\beta}}{\operatorname{argmax}}(\prod _i P(Y_i|\boldsymbol{X}_i,\boldsymbol{\beta})\prod _j P(\beta_i)) \\\
&= \underset{\boldsymbol{\beta}}{\operatorname{argmax}}(-\sum _i\ln(\sigma \sqrt{2\pi}) -\frac{1} {2\sigma^2}\sum _i\lVert \boldsymbol{X}_i ^\mathsf{T} \boldsymbol{\beta}-Y_i\rVert^2 - \sum _j \ln(2b) - \sum _j \frac{|\beta_j-\mu|} {b}\\\
&= \underset{\boldsymbol{\beta}}{\operatorname{argmin}}(\sum _i \lVert \boldsymbol{X}_i ^\mathsf{T} \boldsymbol{\beta}-Y_i\rVert^2) + \frac{2\sigma^2} {b} \sum _j |\beta_j-\mu|
\end{aligned}
\]
若取\(\mu=0, b=\frac{2\sigma^2}{\lambda}\),则
\[
\boldsymbol{\beta}^* = \underset{\boldsymbol{\beta}}{\operatorname{argmin}}(\sum_i \lVert \boldsymbol{X}_i ^\mathsf{T} \boldsymbol{\beta}-Y_i\rVert^2) + \lambda \sum_j |\beta_j-\mu|
\]
即带有 L1 正则项的 Lasso 回归。
高斯先验等价于带有 L2 正则项的岭回归
若对\(\boldsymbol{\boldsymbol{\beta}}\)的每个分量\(\beta_j, j=1,2,\cdots,p\)(\(p\)为\(\boldsymbol{X}\)的维数)施加高斯先验\(N(0, \delta^2)\)
\[
P(\beta_j) = \frac{1} {\sqrt{2\pi}\delta} e^{-\frac{\beta_{j} ^{2}} {2 \delta ^{2} }}
\]
则\(\boldsymbol{\beta}\)的后验分布为
\[
P(\boldsymbol{\beta} | \boldsymbol{X},\boldsymbol{Y}) \propto P(\boldsymbol{Y}|\boldsymbol{X},\boldsymbol{\beta}) P(\boldsymbol{\beta})
\]
最大化后验分布,求得最优的\(\boldsymbol{\beta}\),即
\[
\begin{aligned}
\boldsymbol{\beta}^* &= \underset{\boldsymbol{\beta}}{\operatorname{argmax}}(\prod _i P(Y_i|\boldsymbol{X}_i,\boldsymbol{\beta})\prod _j P(\beta_i)) \\\
&= \underset{\boldsymbol{\beta}}{\operatorname{argmax}}(-\sum _i\ln(\sigma \sqrt{2\pi}) -\frac{1} {2\sigma^2}\sum _i\lVert \boldsymbol{X}_i ^\mathsf{T} \boldsymbol{\beta}-Y_i\rVert^2 -\sum _j\ln(\sqrt{2\pi}\delta) -\sum _j\frac{\beta_j^2} {2 \delta ^2 }
\\\
&= \underset{\boldsymbol{\beta}}{\operatorname{argmin}}(\sum _i \lVert \boldsymbol{X}_i ^\mathsf{T} \boldsymbol{\beta}-Y_i\rVert^2) + \frac{\sigma^2} {\delta ^2} \sum _j \beta_j^2
\end{aligned}
\]
若取\(\mu=0, \delta^2=\frac{\sigma^2}{\lambda}\),则
\[
\boldsymbol{\beta}^* = \underset{\boldsymbol{\beta}}{\operatorname{argmin}}(\sum _i \lVert \boldsymbol{X}_i ^\mathsf{T} \boldsymbol{\beta}-Y_i\rVert^2) + \lambda \sum _j \beta_j ^2
\]
即带有 L2 正则项的岭回归。

