基于 qstock 实现条件选股回测¶

基于 qstock 获取多只股票的历史价格数据，对选股结果进行定期调仓回测。

Equity Curve

导入包和定义获取、处理数据、绩效评价和绘图等函数¶

qstock由“Python 金融量化”公众号开发，可用于获取各个市场的实时和历史数据。本文基于 qstock 获取历史数据，对选股结果进行回测。

Python

# 导入包
import pandas as pd
import qstock as qs
from tqdm import tqdm
import warnings
from highcharts import Highstock


# 定义函数
# 获取调仓日以及持仓的股票
def get_change_position_date_and_stocks(selected_stocks):
    # 根据报告期对应的截至日期，提取出每季度选出的股票代码
    report_date_and_stocks = (
        selected_stocks.groupby("报告日期的截止日")["股票代码"]
        .apply(lambda g: g.values.tolist())
        .to_dict()
    )
    # 将报告报告期对应的截至日期转换为调仓日期
    change_position_date_list = []
    for report_date in report_date_and_stocks.keys():
        # 若报告期的截止日是第一季度的最后一天，则对应的调仓日是4月30日
        if report_date.month == 3:
            change_position_date = "{}{}{}".format(report_date.year, "04", "30")
        # 若报告期的截止日是第二季度的最后一天，则对应的调仓日是8月31日
        elif report_date.month == 6:
            change_position_date = "{}{}{}".format(report_date.year, "08", "31")
        # 若报告期的截止日是第三季度的最后一天，则对应的调仓日是10月31日
        elif report_date.month == 9:
            change_position_date = "{}{}{}".format(report_date.year, "10", "31")
        else:
            raise ValueError
        change_position_date_list.append(change_position_date)
    change_position_date_and_stocks = dict(
        zip(change_position_date_list, report_date_and_stocks.values())
    )
    return change_position_date_and_stocks


# 获取多只股票的每日收盘价格
def get_price_of_many_stocks(code_list, start, end):
    price = pd.DataFrame()
    for code in tqdm(code_list, leave=False):
        price_stock = qs.get_data(
            code_list=code, start=start, end=end, freq="d", fqt=2
        )["close"]
        price_stock.name = code
        price = pd.concat([price, price_stock], axis=1)
    return price


# 将收益率数据转换为价格数据
def prices_from_returns(returns):
    ret = 1 + returns
    ret.iloc[0] = 1
    return ret.cumprod()


# 计算策略评价指标
def strategy_evaluate(equity):
    """
    :param equity:  每天的资金曲线
    :return:
    """

    # ===新建一个dataframe保存回测指标
    results = pd.DataFrame()

    # 将数字转为百分数
    def num_to_pct(value):
        return "%.2f%%" % (value * 100)

    # ===计算累积净值
    results.loc[0, "累积净值"] = round(equity["组合净值"].iloc[-1], 2)

    # ===计算年化收益
    annual_return = (equity["组合净值"].iloc[-1]) ** (
        1 / (equity["交易日期"].iloc[-1] - equity["交易日期"].iloc[0]).days * 365
    ) - 1
    results.loc[0, "年化收益"] = str(round(annual_return * 100, 2)) + "%"

    # ===计算最大回撤，最大回撤的含义：《如何通过3行代码计算最大回撤》https://mp.weixin.qq.com/s/Dwt4lkKR_PEnWRprLlvPVw
    # 计算当日之前的资金曲线的最高点
    equity["max2here"] = equity["组合净值"].expanding().max()
    # 计算到历史最高值到当日的跌幅，drowdwon
    equity["dd2here"] = equity["组合净值"] / equity["max2here"] - 1
    # 计算最大回撤，以及最大回撤结束时间
    end_date, max_draw_down = tuple(
        equity.sort_values(by=["dd2here"]).iloc[0][["交易日期", "dd2here"]]
    )
    # 计算最大回撤开始时间
    start_date = (
        equity[equity["交易日期"] <= end_date]
        .sort_values(by="组合净值", ascending=False)
        .iloc[0]["交易日期"]
    )
    # 将无关的变量删除
    equity.drop(["max2here", "dd2here"], axis=1, inplace=True)
    results.loc[0, "最大回撤"] = format(max_draw_down, ".2%")
    results.loc[0, "最大回撤开始时间"] = str(start_date)
    results.loc[0, "最大回撤结束时间"] = str(end_date)

    # ===年化收益/回撤比：
    results.loc[0, "年化收益/回撤比"] = round(annual_return / abs(max_draw_down), 2)

    # ===每年、每月收益率
    equity.set_index("交易日期", inplace=True)
    year_return = (
        equity[["组合收益率", "指数收益率"]]
        .resample(rule="A")
        .apply(lambda x: (1 + x).prod() - 1)
    )
    monthly_return = (
        equity[["组合收益率", "指数收益率"]]
        .resample(rule="M")
        .apply(lambda x: (1 + x).prod() - 1)
    )

    year_return["超额收益"] = year_return["组合收益率"] - year_return["指数收益率"]
    monthly_return["超额收益"] = monthly_return["组合收益率"] - monthly_return["指数收益率"]

    year_return["组合收益率"] = year_return["组合收益率"].apply(num_to_pct)
    year_return["指数收益率"] = year_return["指数收益率"].apply(num_to_pct)
    year_return["超额收益"] = year_return["超额收益"].apply(num_to_pct)

    monthly_return["组合收益率"] = monthly_return["组合收益率"].apply(num_to_pct)
    monthly_return["指数收益率"] = monthly_return["指数收益率"].apply(num_to_pct)
    monthly_return["超额收益"] = monthly_return["超额收益"].apply(num_to_pct)

    return results.T, year_return, monthly_return


# 绘制净值曲线
def draw_equity_curve(
    prices, returns_data=False, title="Equity Curve", output_path=None
):
    # 将传入的数据修改为数据框
    if not isinstance(prices, pd.DataFrame):
        warnings.warn("prices are not in a dataframe", RuntimeWarning)
        prices = pd.DataFrame(prices)
    # 将索引修改为日期时间格式
    if not isinstance(prices.index, pd.DatetimeIndex):
        prices.index = pd.to_datetime(prices.index)
    # 如果传入的是收益率数据，则需要转换成价格数据
    if returns_data:
        prices = prices_from_returns(prices)
    # 初始化绘图对象
    H = Highstock()
    # 导入每一个资产的价格数据
    for column in prices.columns:
        H.add_data_set(
            data=prices[column].reset_index().values.tolist(),
            series_type="line",
            name=column,
        )
    # 设置绘图参数
    options = {
        "title": {"text": title},
        "rangeSelector": {"selected": 5},  # 1-5的数字代表默认观察窗口为1m、3m、6m、YTM、1y和All
        "yAxis": {
            "labels": {
                "formatter": "function () {\
                                return (this.value > 0 ? ' + ' : '') + this.value + '%';\
                            }"
            },  # this.value > 0 ? ' + '可以在正收益的数值前加上“+”
            # 绘制纵轴为0的横线
            "plotLines": [{"value": 0, "width": 2, "color": "silver"}],
        },
        "plotOptions": {"series": {"compare": "percent"}},
        "tooltip": {
            "pointFormat": '<span style="color:{series.color}">{series.name}:</span> <b>{point.y}</b> ({point.change}%)<br/>',
            "valueDecimals": 2,  # 默认显示的小数位
        },
    }
    # 应用绘图参数
    H.set_dict_options(options)
    # 如果指定了输出路径，则输出html文件到这个路径
    if output_path:
        f = open("{}.html".format(output_path), "w")
        f.write(H.htmlcontent)
        f.close()
    return H

Python

# 读取历史选股数据（每季度 15 只）
selected_stocks = pd.read_csv(
    "./selected_stocks.csv", parse_dates=["报告日期的截止日"], encoding="gbk"
)  # parse_dates 将'报告日期的截止日'这一列识别为日期格式，gbk 编码支持中文
# 截取“股票代码”和“报告日期的截止日”这两列
selected_stocks = selected_stocks[["股票代码", "报告日期的截止日"]]
# 将“股票代码”的后缀“.SH”去掉
selected_stocks["股票代码"] = selected_stocks["股票代码"].apply(lambda x: x[:-3])
# 获取调仓日以及持仓的股票
change_position_date_and_stocks = get_change_position_date_and_stocks(selected_stocks)
# 获取调仓日的列表
change_position_date_list = list(change_position_date_and_stocks.keys())

计算组合收益率（使用简单加权的粗略算法）¶

使用简单加权的粗略算法计算组合收益率，这一方法存在一定的缺陷。

例如，若资产组合包含两个资产，第一个资产每天的收益率都是\(-10\%\)，第二个资产每天的收益率都是\(+10\%\)。

按照简单加权的粗略算法，第一天，第一个资产的价格变成了\(1\times(1-10\%)=0.9\)，第二个资产的价格变成了\(1\times(1+10\%)=1.1\)，因此资产组合的净值是\(\frac{0.9+1.1}{2}=1\)。根据简单加权的粗略算法，资产组合在第一天的收益率是\(\frac{-10\%+10\%}{2}=0\)。这个结果在第一天确实是对的。

但是，第二天的时候，第一个资产的价格变成了\(0.9\times(1-10\%)=0.81\)，第二个资产的价格变成了\(1.1\times(1+10\%)=1.21\)，因此资产组合的净值是\(\frac{0.81+1.21}{2}=1.005\)，因此资产组合在第二天的收益率是 0.5%。但是，根据简单加权的粗略算法，资产组合在第一天的收益率仍然是\(\frac{-10\%+10\%}{2}=0\)。

造成这一差异的根本原因在于，资产组合内部的权重是会随着各资产的涨跌而改变的。一个资产上涨得越多，它的涨跌幅对整个资产组合涨跌幅的影响也越大。

这里为了简便，只使用简单加权的粗略算法计算组合收益率。更为精确的算法可以是：将各股票看作是投资组合的一部分，每天跟踪这一部分净值的变化，到下一调仓日再将各部分的净值相加，即得到整个投资组合的净值。

Python

# 创建空数据框，用于存放组合收益率
portfolio_return = pd.DataFrame()
# 对每一个调仓日，获取当日的股票价格，将价格转换为收益率，并计算组合在这段持有期的收益率
pbar = tqdm(change_position_date_list)
for change_position_date in pbar:
    pbar.set_description("正在计算从%s开始的组合每日收益率" % change_position_date)
    # 获取这一个调仓日至下一个调仓日之间的持仓股票价格
    code_list = change_position_date_and_stocks[change_position_date]
    # 获取下一个调仓日
    if (
        change_position_date == change_position_date_list[-1]
    ):  # 如果是最后一个调仓日，则下一个调仓日在change_position_date_list中找不到，需要手动设置为2022年8月31日
        next_change_position_date = "20220831"
    else:  # 否则下一个调仓日可以直接在change_position_date_list中找到
        next_change_position_date = change_position_date_list[
            change_position_date_list.index(change_position_date) + 1
        ]
    # 获取这一个调仓日至下一个调仓日之间的持仓股票价格
    stock_price = get_price_of_many_stocks(
        code_list=code_list, start=change_position_date, end=next_change_position_date
    )  # fqt=2表示后复权
    # 将价格转换为收益率，且删除全是空值的行（即第一行）
    stock_return = stock_price.pct_change().dropna(how="all")
    # 对收益率进行加权求和，得到组合收益率，并将结果添加到portfolio_return中
    portfolio_return_in_this_quarter = stock_return.mul(
        1 / len(stock_return.columns), axis=1
    ).sum(axis=1)
    portfolio_return = pd.concat(
        [portfolio_return, portfolio_return_in_this_quarter], axis=0
    )

正在计算从20220430开始的组合每日收益率: 100%|██████████| 37/37 [01:11<00:00, 1.94s/it]

获取组合净值和基准指数净值¶

Python

# 将组合收益率转换为累计净值
portfolio_net_value = prices_from_returns(portfolio_return)
# 修改列名
portfolio_net_value.columns = ["组合净值"]
# 修改索引名
portfolio_net_value.index.name = "date"

Python

# 获取中证500指数的价格
index_price = qs.get_price(
    code_list=["中证500"], start="20100504", end="20220831", freq="d", fqt=2
)
# 将中证500指数的价格归一化
index_price = index_price.div(index_price.iloc[0])

100%|██████████| 1/1 [00:00<00:00, 1004.38it/s]

Python

# 将组合收益率和中证 500 指数的价格合并
equity = portfolio_net_value.merge(
    index_price, how="left", left_index=True, right_index=True
)

绘制净值曲线¶

Python

# 绘制组合净值和中证500指数的净值曲线
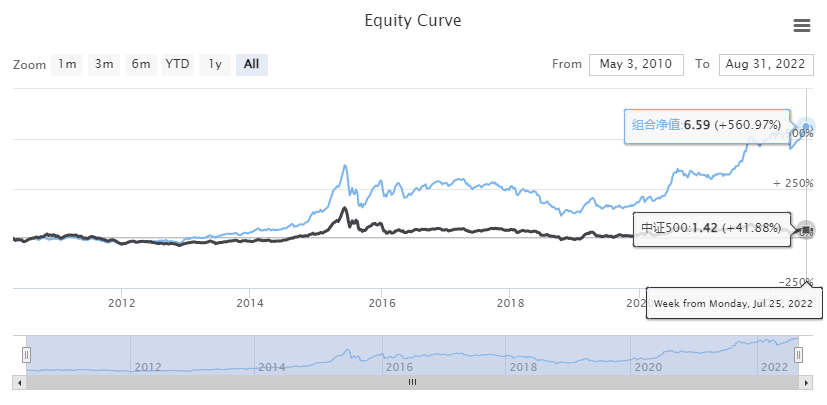
draw_equity_curve(equity)

Equity Curve

Python

# 修改列名
equity.rename(columns={"中证 500": "指数收益率"}, inplace=True)
# 计算组合收益率
equity["组合收益率"] = equity["组合净值"].pct_change()
# 计算指数收益率
equity["指数收益率"] = equity["指数收益率"].pct_change()
# 生成交易日期列
equity["交易日期"] = equity.index

绩效评价¶

Python

# 计算策略评价指标
overall_performance, year_return, month_return = strategy_evaluate(equity)

Python

overall_performance

	0
累积净值	6.31
年化收益	16.11%
最大回撤	-56.75%
最大回撤开始时间	2015-06-12 00:00:00
最大回撤结束时间	2018-10-18 00:00:00
年化收益/回撤比	0.28

Python

year_return

	组合收益率	指数收益率	超额收益
交易日期
2010-12-31	-3.12%	11.33%	-14.45%
2011-12-31	-26.29%	-33.83%	7.53%
2012-12-31	32.59%	0.28%	32.31%
2013-12-31	36.37%	16.89%	19.48%
2014-12-31	78.17%	39.01%	39.17%
2015-12-31	68.05%	43.12%	24.93%
2016-12-31	-3.76%	-17.78%	14.02%
2017-12-31	-6.39%	-0.20%	-6.19%
2018-12-31	-36.16%	-33.32%	-2.84%
2019-12-31	27.43%	26.38%	1.05%
2020-12-31	49.32%	20.87%	28.45%
2021-12-31	44.83%	15.58%	29.24%
2022-12-31	3.05%	-16.36%	19.40%

Python

month_return

	组合收益率	指数收益率	超额收益
交易日期
2010-05-31	-10.60%	-7.44%	-3.17%
2010-06-30	-8.02%	-10.72%	2.70%
2010-07-31	15.30%	14.37%	0.93%
2010-08-31	10.09%	9.50%	0.59%
2010-09-30	-9.61%	1.55%	-11.16%
...	...	...	...
2022-04-30	-10.71%	-11.02%	0.31%
2022-05-31	4.69%	7.08%	-2.38%
2022-06-30	5.59%	7.10%	-1.51%
2022-07-31	6.65%	-2.48%	9.13%
2022-08-31	-4.40%	-2.20%	-2.20%

148 rows × 3 columns

基于 qstock 实现条件选股回测¶

导入包和定义获取、处理数据、绩效评价和绘图等函数¶

计算组合收益率（使用简单加权的粗略算法）¶

获取组合净值和基准指数净值¶

绘制净值曲线¶

绩效评价¶

评论