神经网络中的激活函数

激活函数在神经元中是非常重要的。为了增强网络的表示能力和学习能力，激活函数需要具备以下几点性质：

1. 连续并可导（允许少数点上不可导）的 非线性函数 （若激活函数仍是线性函数，那么再多层的神经网络都只能拟合一个线性函数）。可导的激活函数可以直接利用数值优化的方法来学习网络参数。
2. 激活函数及其导函数要尽可能的简单，有利于提高网络计算效率。
3. 激活函数的导函数的值域要在一个合适的区间内，不能太大也不能太小，否则会影响训练的效率和稳定性。

本文总结了神经网络中常见的激活函数。

Logistic 函数

Logistic 函数是 Sigmoid 函数的一种，其定义为：

\[ \sigma(x) = \frac{1}{1 + e^{-x}} \]

Logistic 函数的导函数为：

\[ \begin{aligned} \sigma^{'}(x) &=\frac{e^{-x}}{(1 + e^{-x})^2}\\ &= \frac{1}{1 + e^{-x}} \frac{e^{-x}}{1 + e^{-x}}\\ &= {\color{red}{\sigma(x) (1 - \sigma(x))}} \end{aligned} \]

快速计算 Logistic 函数的导数

上式最后一行表明，Logistic 函数的导函数可以用 Sigmoid 函数本身来表示，即：

\[ \sigma^{'}(x) = \sigma(x) (1 - \sigma(x)) \]

可以用这个性质快速计算 Sigmoid 函数的导数。

Tanh 函数

Tanh 函数的定义为：

\[ tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}} \]

Tanh 函数可以看作是 Logistic 函数的伸缩平移变换，即：

\[ tanh(x) = 2 \sigma(2x) - 1 \]

Tanh 函数的导函数为：

\[ \begin{aligned} \tanh^{'}(x) &= \frac{(e^x + e^{-x})(e^x + e^{-x}) - (e^x - e^{-x})(e^x - e^{-x})}{(e^x + e^{-x})^2}\\ &= \frac{(e^x + e^{-x})^2 - (e^x - e^{-x})^2}{(e^x + e^{-x})^2}\\ &= 1 - \frac{(e^x - e^{-x})^2}{(e^x + e^{-x})^2}\\ &= {\color{red}{1 - \tanh^2(x)}} \end{aligned} \]

快速计算 Tanh 函数的导数

上式最后一行表明，Tanh 函数的导函数可以用 Tanh 函数本身来表示，即：

\[ \tanh^{'}(x) = 1 - \tanh^2(x) \]

可以用这个性质快速计算 Tanh 函数的导数。

Sigmoid 型函数

Sigmoid 型函数是指一类 S 型曲线函数，为两端饱和函数。

对于函数 \(f(x)\)，

• 若 \(x \rightarrow - \infty\) 时，\(f^{'}(x) \rightarrow 0\)，称为左饱和。
• 若 \(x \rightarrow + \infty\) 时，\(f^{'}(x) \rightarrow 0\)，称为右饱和。
• 当同时满足左右饱和时，称为两端饱和。

常用的 Sigmoid 型函数有上述的 Logistic 函数和 Tanh 函数。

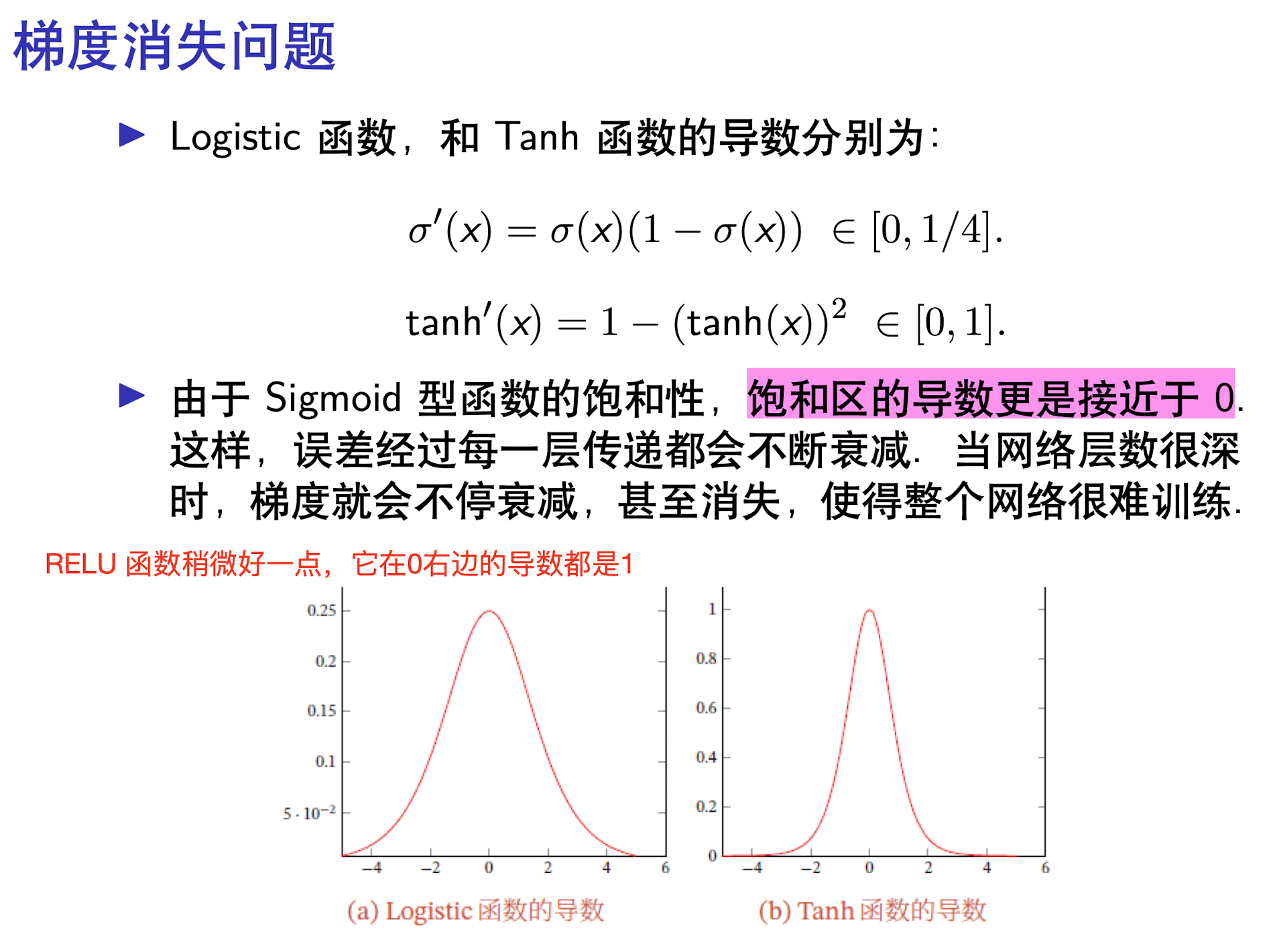
Sigmoid 型函数的梯度消失问题

ReLU 函数

ReLU 也叫修正线性单元（Rectified Linear Unit），其定义为：

\[ \begin{aligned} ReLU(x) &= \begin{cases} x & x \geq 0 \\ 0 & x<0 \end{cases} \\ &= \max(0, x) \end{aligned} \]

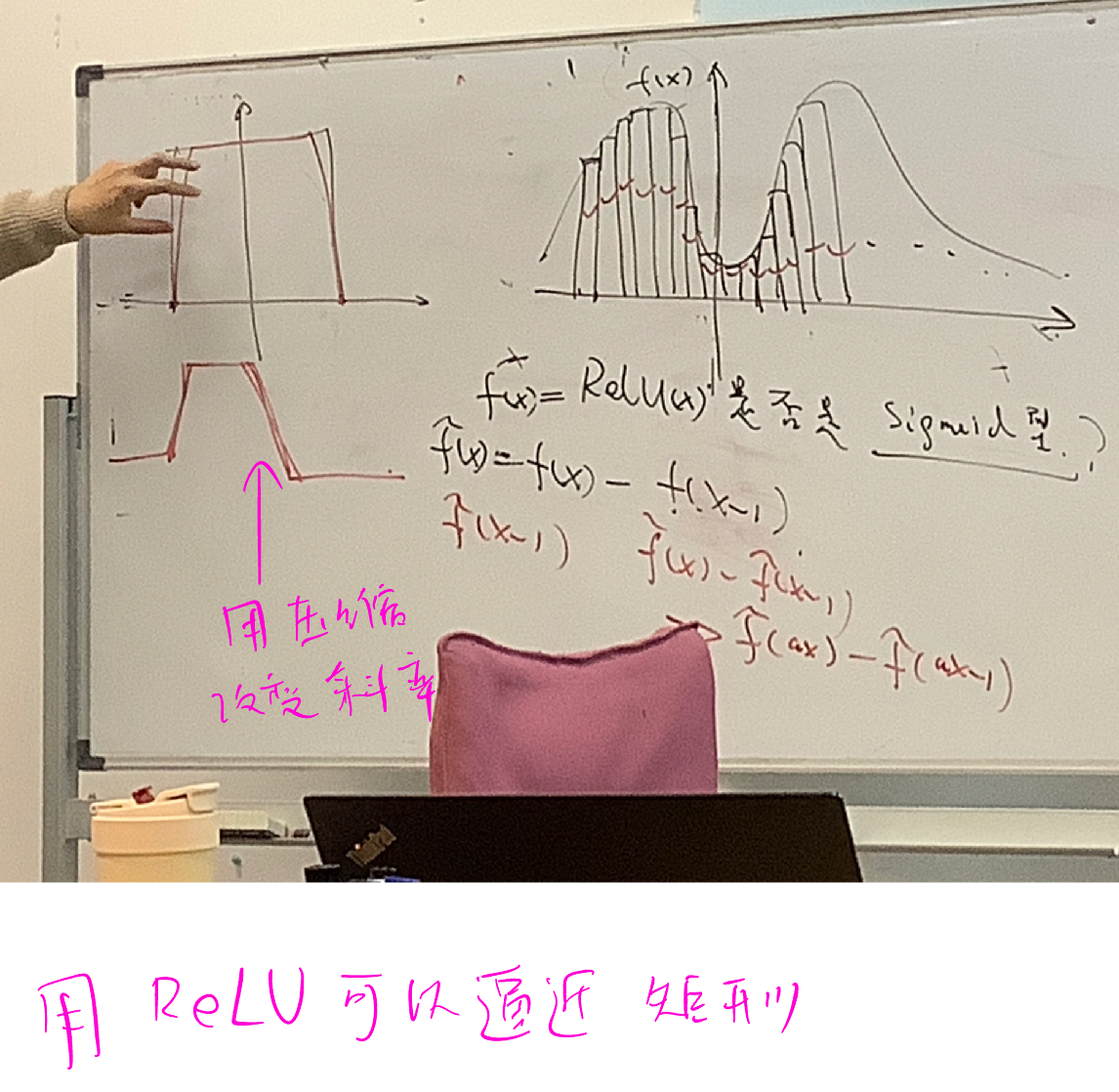
ReLU 函数虽然不是 Sigmoid 型的，但构造 \(f(x) - f(x-1)\) 就可以满足 Sigmoid 型函数的定义。

利用类似的思想，我们可以用 ReLU 函数逼近任意矩形。

ReLU 函数的优缺点：

Leaky ReLU 函数

带泄露的 ReLU（Leaky ReLU）在输入 \(x < 0\) 时，保持一个很小的梯度 \(\gamma\)。这样当神经元非激活时也能有一个非零的梯度可以更新参数，避免永远不能被激活的情况。

Leaky ReLU 函数的定义为：

\[ \begin{aligned} LeakyReLU(x) &= \begin{cases} x & x \geq 0 \\ \gamma x & x<0 \end{cases} \\ &= \max(\gamma x, x) \end{aligned} \]

\(\gamma\) 通常很小，如 \(0.01\)。

Softplus 函数

Softplus 函数可以看作是 ReLU 函数的平滑版本，其定义为：

\[ \text{softplus}(x) = \log(1 + e^x) \]

Softplus 函数的导函数刚好是 Sigmoid 函数。Softplus 函数虽然也具有单侧抑制、宽兴奋边界的特性，却没有稀疏激活性。

Maxout 函数

Maxout 函数是一种非线性函数，其定义为：

\[ \begin{aligned} \text{maxout}(x) &= \underset{k}{\max}~~ z_k(x)\\ &= \max\left(\begin{matrix} w_1^T x + b_1\\ w_2^T x + b_2\\ \vdots\\ w_k^T x + b_k \end{matrix}\right) \end{aligned} \]

这个激活函数不像前几个函数一样有明确的表达式，而是要学习 \(k\) 组参数，再选一个最大的输出值作为激活值。这就是为什么采用 Maxout 的时候，参数个数成 k 倍增加的原因。本来我们只需要一组参数就够了，采用 Maxout 后，就需要有 k 组参数。

更多理解可以参考：https://blog.csdn.net/hjimce/article/details/50414467，写得非常好。

评论