方差缩减技术之条件期望法¶
使用条件期望法降低蒙特卡洛模拟得到的估计量的方差。
Python
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from tqdm import tqdm
from scipy.stats import gamma
np.random.seed(0)
问题描述¶


方差缩减技术——条件期望法¶
后验分布¶

Python
Number = np.array(
[
38,
1,
13,
36,
24,
3,
15,
34,
22,
5,
17,
32,
20,
7,
11,
30,
26,
9,
28,
37,
2,
14,
35,
23,
4,
16,
33,
21,
6,
18,
31,
19,
8,
12,
29,
25,
10,
27,
]
)
Wheel1 = np.array(
[
2127,
2082,
2110,
2221,
2192,
2008,
2035,
2113,
2099,
2199,
2044,
2133,
1912,
1999,
1974,
2051,
1984,
2053,
2019,
2046,
1999,
2168,
2150,
2041,
2047,
2091,
2142,
2196,
2153,
2191,
2192,
2284,
2136,
2110,
2032,
2188,
2121,
2158,
]
)
wheel2 = np.array(
[
1288,
1234,
1261,
1251,
1164,
1438,
1264,
1335,
1342,
1232,
1326,
1302,
1227,
1192,
1278,
1336,
1296,
1298,
1205,
1189,
1171,
1279,
1315,
1296,
1256,
1304,
1304,
1351,
1281,
1392,
1306,
1330,
1266,
1224,
1190,
1229,
1320,
1336,
]
)
wheel = pd.DataFrame({"Wheel1": Wheel1, "Wheel2": wheel2}, index=Number)
wheel.sort_index(inplace=True)
Wheel 1¶
自然的 Monte Carlo 方法¶
模拟 Dirichlet 分布的随机数¶
计算\(\mu\)的估计值及其\(95\%\)置信区间¶
Python
def naive_nonte_carlo(n):
df = pd.DataFrame(np.random.dirichlet(wheel["Wheel1"], size=n), columns=wheel.index)
df["p19>max(pi)"] = df.apply(lambda x: x[19] > max(x[x.index != 19]), axis=1)
mu = df["p19>max(pi)"].mean()
return mu
Python
mu_list_maive_monte_carlo = []
for simulation in tqdm(range(1000)):
mu = naive_nonte_carlo(n)
mu_list_maive_monte_carlo.append(mu)
Text Only
100%|██████████| 1000/1000 [00:12<00:00, 78.60it/s]
Python
mu_mean_maive_monte_carlo = np.mean(mu_list_maive_monte_carlo)
mu_std_maive_monte_carlo = np.std(mu_list_maive_monte_carlo)
left = mu_mean_maive_monte_carlo - 1.96 * mu_std_maive_monte_carlo
right = mu_mean_maive_monte_carlo + 1.96 * mu_std_maive_monte_carlo
print("mu 的估计值为:{:.4f}".format(mu_mean_maive_monte_carlo))
print("95% 置信水平的置信区间为:({:.4f}, {:.4f})".format(left, right))
Text Only
mu的估计值为:0.6318
95%置信水平的置信区间为:(0.5378, 0.7259)
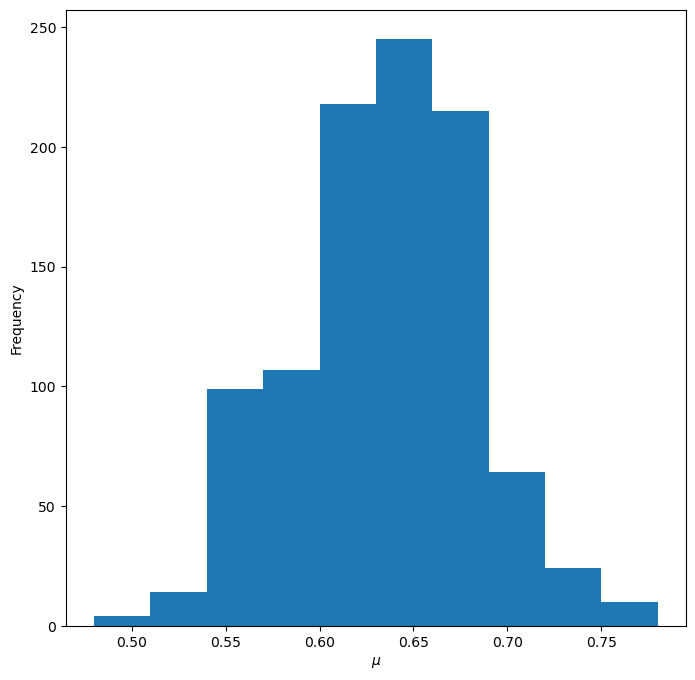
画出 Monte Carlo 估计的直方图¶
Python
fig = plt.figure(figsize=(8, 8))
ax = fig.add_subplot(111)
plt.hist(mu_list_maive_monte_carlo)
ax.set_xlabel(r"$\mu$")
ax.set_ylabel("Frequency")
plt.show()
条件期望法¶
这里有点疑问,我不知道怎么计算当给定\(p^{19}\)时,其他\(p\)小于\(p^{19}\)的条件期望。代码中用的是独立分布的 CDF 值相乘,但实际上各个变量之间是相关的,并不是独立分布的。
对每一个 wheel_19,求条件期望¶
Python
def less_than_q19():
# 用 gamma 分布生成 wheel_19
wheel_19 = np.random.gamma(shape=wheel["Wheel1"][19] + 1)
less_than_q19 = 1
# 对每一个 q_i,生成 gamma 分布,然后计算 wheel_i<wheel_19 的概率
for i in range(1, 38 + 1):
if i != 19:
wheel_i_less_than_q19 = gamma.cdf(wheel_19, wheel["Wheel1"][i] + 1)
less_than_q19 *= wheel_i_less_than_q19
return less_than_q19
Python
mu_list_conditional_expectation = []
for simulation in tqdm(range(1000)):
less_than_q19_list = []
for i in range(n):
less_than_q19_value = less_than_q19()
less_than_q19_list.append(less_than_q19_value)
mu = np.mean(less_than_q19_list)
mu_list_conditional_expectation.append(mu)
Text Only
100%|██████████| 1000/1000 [09:27<00:00, 1.76it/s]
计算\(\mu\)的估计值及其\(95\%\)置信区间¶
Python
mu_mean_conditional_expectation = np.mean(mu_list_conditional_expectation)
mu_std_conditional_expectation = np.std(mu_list_conditional_expectation)
left = mu_mean_conditional_expectation - 1.96 * mu_std_conditional_expectation
right = mu_mean_conditional_expectation + 1.96 * mu_std_conditional_expectation
print("mu 的估计值为:{:.4f}".format(mu_mean_conditional_expectation))
print("95% 置信水平的置信区间为:({:.4f}, {:.4f})".format(left, right))
Text Only
mu的估计值为:0.6299
95%置信水平的置信区间为:(0.5631, 0.6968)
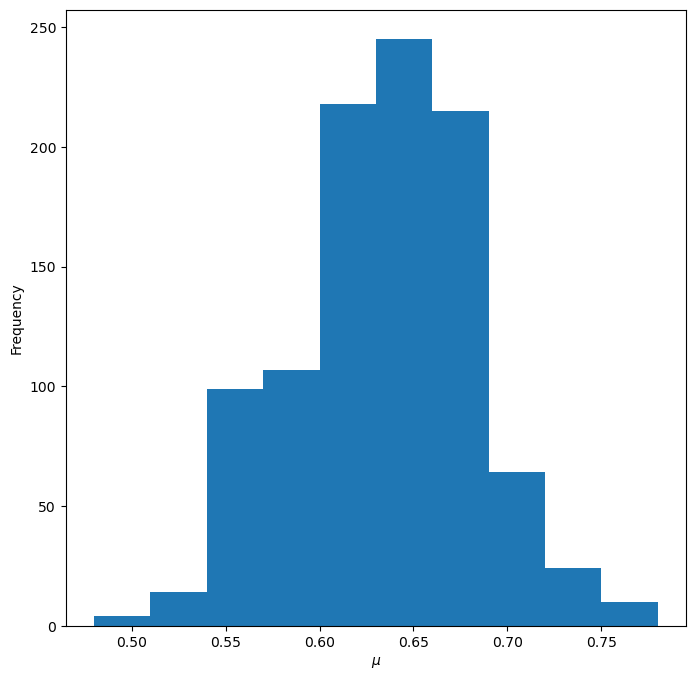
画出条件期望法估计的直方图¶
Python
fig = plt.figure(figsize=(8, 8))
ax = fig.add_subplot(111)
plt.hist(mu_list_conditional_expectation)
ax.set_xlabel(r"$\mu$")
ax.set_ylabel("Frequency")
plt.show()
比较两种方法的方差¶
Python
print("自然的 Monte Carlo 方法的估计值的方差为:{:.4f}".format(mu_std_maive_monte_carlo))
print("条件期望法的估计值的方差为:{:.4f}".format(mu_std_conditional_expectation))
Text Only
自然的Monte Carlo方法的估计值的方差为:0.0480
条件期望法的估计值的方差为:0.0341
条件期望法的结果比自然的 Monte Carlo 方法的方差更小。
Wheel 2¶
自然的 Monte Carlo 方法¶
模拟 Dirichlet 分布的随机数¶
计算\(\mu\)的估计值及其\(95\%\)置信区间¶
Python
def naive_nonte_carlo(n):
df = pd.DataFrame(np.random.dirichlet(wheel["Wheel2"], size=n), columns=wheel.index)
df["p3>max(pi)"] = df.apply(lambda x: x[3] > max(x[x.index != 3]), axis=1)
mu = df["p3>max(pi)"].mean()
return mu
Python
mu_list_maive_monte_carlo = []
for simulation in tqdm(range(1000)):
mu = naive_nonte_carlo(n)
mu_list_maive_monte_carlo.append(mu)
Text Only
100%|██████████| 1000/1000 [00:14<00:00, 70.42it/s]
Python
mu_mean_maive_monte_carlo = np.mean(mu_list_maive_monte_carlo)
mu_std_maive_monte_carlo = np.std(mu_list_maive_monte_carlo)
left = mu_mean_maive_monte_carlo - 1.96 * mu_std_maive_monte_carlo
right = mu_mean_maive_monte_carlo + 1.96 * mu_std_maive_monte_carlo
print("mu 的估计值为:{:.4f}".format(mu_mean_maive_monte_carlo))
print("95% 置信水平的置信区间为:({:.4f}, {:.4f})".format(left, right))
Text Only
mu的估计值为:0.7401
95%置信水平的置信区间为:(0.6578, 0.8224)
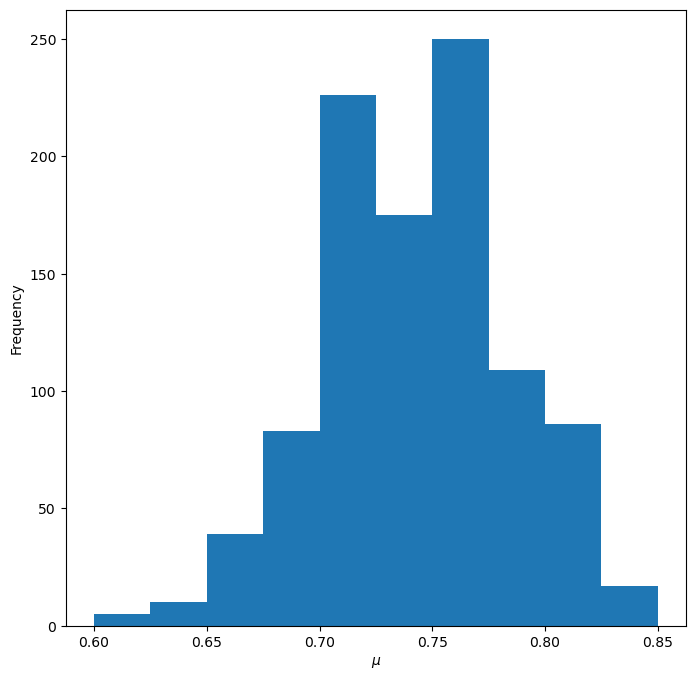
画出 Monte Carlo 估计的直方图¶
Python
fig = plt.figure(figsize=(8, 8))
ax = fig.add_subplot(111)
plt.hist(mu_list_maive_monte_carlo)
ax.set_xlabel(r"$\mu$")
ax.set_ylabel("Frequency")
plt.show()
条件期望法¶
对每一个 wheel_3,求条件期望¶
Python
def less_than_q3():
# 用 gamma 分布生成 wheel_3
wheel_3 = np.random.gamma(shape=wheel["Wheel2"][3] + 1)
less_than_q3 = 1
# 对每一个 q_i,生成 gamma 分布,然后计算 wheel_i<wheel_3 的概率
for i in range(1, 38 + 1):
if i != 3:
wheel_i_less_than_q3 = gamma.cdf(wheel_3, wheel["Wheel2"][i] + 1)
less_than_q3 *= wheel_i_less_than_q3
return less_than_q3
Python
mu_list_conditional_expectation = []
for simulation in tqdm(range(1000)):
less_than_q3_list = []
for i in range(n):
less_than_q3_value = less_than_q3()
less_than_q3_list.append(less_than_q3_value)
mu = np.mean(less_than_q3_list)
mu_list_conditional_expectation.append(mu)
Text Only
100%|██████████| 1000/1000 [08:54<00:00, 1.87it/s]
计算\(\mu\)的估计值及其\(95\%\)置信区间¶
Python
mu_mean_conditional_expectation = np.mean(mu_list_conditional_expectation)
mu_std_conditional_expectation = np.std(mu_list_conditional_expectation)
left = mu_mean_conditional_expectation - 1.96 * mu_std_conditional_expectation
right = mu_mean_conditional_expectation + 1.96 * mu_std_conditional_expectation
print("mu 的估计值为:{:.4f}".format(mu_mean_conditional_expectation))
print("95% 置信水平的置信区间为:({:.4f}, {:.4f})".format(left, right))
Text Only
mu的估计值为:0.7393
95%置信水平的置信区间为:(0.6828, 0.7959)
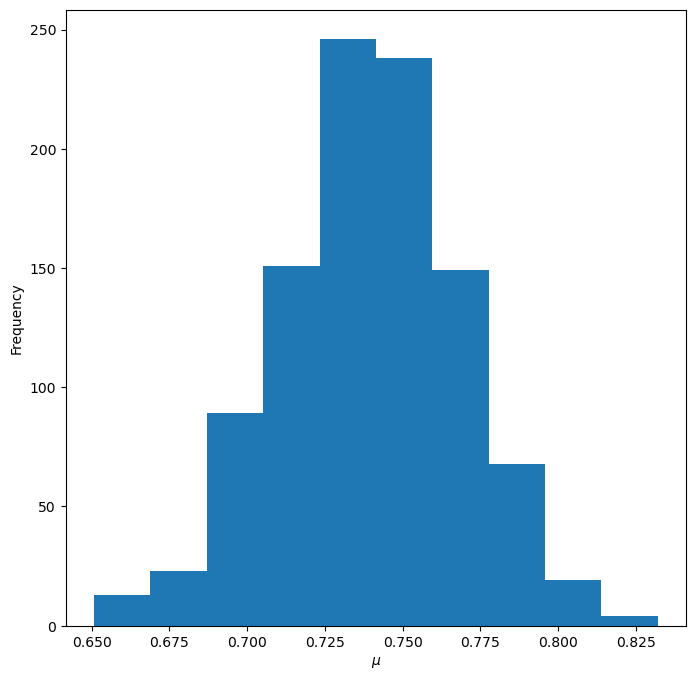
画出条件期望法估计的直方图¶
Python
fig = plt.figure(figsize=(8, 8))
ax = fig.add_subplot(111)
plt.hist(mu_list_conditional_expectation)
ax.set_xlabel(r"$\mu$")
ax.set_ylabel("Frequency")
plt.show()
比较两种方法的方差¶
Python
print("自然的 Monte Carlo 方法的估计值的方差为:{:.4f}".format(mu_std_maive_monte_carlo))
print("条件期望法的估计值的方差为:{:.4f}".format(mu_std_conditional_expectation))
Text Only
自然的Monte Carlo方法的估计值的方差为:0.0420
条件期望法的估计值的方差为:0.0288
条件期望法的结果比自然的 Monte Carlo 方法的方差更小。