随机抽样之 MCMC 算法¶
MCMC 算法是一种随机抽样算法。借助建议分布,可以在各个样本状态之间进行转移,最终得到目标分布的样本。本文使用了逐分量 MCMC、随机游走和独立性抽样构造 Ising 分布和二元正态分布的随机样本。
Python
# 导入包
import numpy as np
# 设置随机数种子
np.random.seed(0)
from scipy.stats import multivariate_normal
import matplotlib.pyplot as plt
plt.rcParams["font.sans-serif"] = ["simsun"]
plt.rcParams["axes.unicode_minus"] = False
from tqdm import tqdm
Ising 模型¶

算法¶

定义目标分布的概率密度函数¶
Python
def pi(vector_x):
sum_x_i__times_x_i_plus_1 = 0
for i in range(len(vector_x) - 1):
sum_x_i__times_x_i_plus_1 += vector_x[i] * vector_x[i + 1]
return np.exp(sum_x_i__times_x_i_plus_1)
定义接受率函数¶
逐分量 Metropolis-Hastings 算法¶
初始化样本¶
Python
# 生成初始向量
vector_x = np.random.randint(2, size=20)
# 将 vector_x 中的 0 替换为 -1
vector_x[vector_x == 0] = -1
# 打印初始向量
print("初始向量为:", vector_x)
Text Only
初始向量为: [ 1 1 -1 -1 -1 -1 -1 -1 -1 -1 1 1 -1 -1 1 -1 -1 1 -1 1]
设定迭代次数¶
迭代产生样本¶
Python
# 不断迭代,生成数量为 iteration 的样本
for t in tqdm(range(iteration)):
# 逐分量更新
for i in range(d):
# 生成一个随机数 y,它来自试投密度函数:y 有 0.5 的概率取值为 1,有 0.5 的概率取值为 -1
u = np.random.uniform(0, 1)
if u < 0.5:
y = 1
else:
y = -1
# 基于接受率,决定是否接受
vector_y_x_i_ = vector_x.copy()
# 将 x_i 的值改为 y
vector_y_x_i_[i] = y
# q(x_i | y, x_{i-}) 和 q(y | x_i, x_{i-}) 的值均为 0.5,可以自动约去
alpha_i = alpha(vector_x, vector_y_x_i_)
# 生成一个随机数 u,它来自均匀分布
u = np.random.uniform(0, 1)
# 如果接受率大于 u,则接受,即更新 x_i 的值为 y
if alpha_i > u:
vector_x[i] = y
accept += 1
# 保存样本
# 第一次迭代时,初始化样本
if t == 0:
samples = vector_x.copy()
# 后续迭代时,将样本添加到样本集中
else:
samples = np.vstack((samples, vector_x))
# 计算接受率
accept_rate = accept / (iteration * d)
print("接受率:{:.2%}".format(accept_rate))
Text Only
100%|██████████| 100000/100000 [03:28<00:00, 479.59it/s]
接受率:61.91%
收敛性诊断——依据各分量的累计均值¶
Text Only
array([[ 1, 1, -1, ..., -1, 1, 1],
[ 2, 2, -2, ..., -2, 0, 2],
[ 3, 3, -1, ..., -3, -1, 3],
...,
[-452, -684, -716, ..., 1600, 2006, 2076],
[-453, -685, -717, ..., 1601, 2007, 2077],
[-454, -686, -718, ..., 1602, 2008, 2078]])
Text Only
array([[ 1],
[ 2],
[ 3],
...,
[ 99998],
[ 99999],
[100000]])

可以看到,当迭代次数达到 50000 时,各分量的累计均值都已经趋于 0,说明样本已经收敛。
二元正态分布¶

设置目标分布的参数¶
Python
mu = np.array([0, 0])
sigma = np.array([[1, 0.7], [0.7, 1]])
# 构造二维正态分布的理论分布
var = multivariate_normal(mean=mu, cov=sigma)
定义二元正态分布的概率密度函数¶
Python
def two_dimensional_gaussian(vector_x_y, mu, sigma):
return (
1
/ (2 * np.pi * np.sqrt(np.linalg.det(sigma)))
* np.exp(
-0.5 * (vector_x_y - mu).T.dot(np.linalg.inv(sigma)).dot(vector_x_y - mu)
)
)
随机游走算法¶


初始化样本¶
Text Only
样本的初始值为: [0 0]
设定迭代次数¶
迭代产生样本¶
Python
for t in tqdm(range(iteration)):
# 生成正态分布随机数
vector_e1_e2_ = np.random.normal(0, 1, 2)
# 将上一步生成的随机数加到 x 和 y 上
vector_x_y_ = vector_x_y + vector_e1_e2_
# 计算接受率
ratio = two_dimensional_gaussian(vector_x_y_, mu, sigma) / two_dimensional_gaussian(
vector_x_y, mu, sigma
)
alpha = min(1, ratio)
# 生成一个随机数 u,它来自均匀分布
u = np.random.uniform(0, 1)
# 如果接受率大于 u,则接受,即更新 x 和 y 的值
if alpha > u:
vector_x_y = vector_x_y_
accept += 1
# 保存样本
# 第一次迭代时,初始化样本
if t == 0:
samples_random_walk = vector_x_y.copy()
# 后续迭代时,将样本添加到样本集中
else:
samples_random_walk = np.vstack((samples_random_walk, vector_x_y))
# 计算接受率
accept_rate = accept / iteration
print("接受率:{:.2%}".format(accept_rate))
Text Only
100%|██████████| 100000/100000 [00:24<00:00, 4091.07it/s]
接受率:45.51%
Text Only
array([[ 0. , 0. ],
[ 0. , 0. ],
[ 0. , 0. ],
...,
[-0.71973486, -1.23049515],
[-0.71973486, -1.23049515],
[ 0.33205658, -0.79309342]])
收敛性诊断——依据各分量的累计均值¶
Text Only
array([[ 0. , 0. ],
[ 0. , 0. ],
[ 0. , 0. ],
...,
[1019.11864357, 1477.36299153],
[1018.39890871, 1476.13249638],
[1018.73096529, 1475.33940296]])
Text Only
array([[ 1],
[ 2],
[ 3],
...,
[ 99998],
[ 99999],
[100000]])
Python
fig = plt.figure(figsize=(10, 6))
plt.plot(cummean, label=["x", "y"])
# 绘制辅助线,纵坐标为 0
plt.axhline(0, color="black", linestyle="--")
plt.legend()
plt.show()
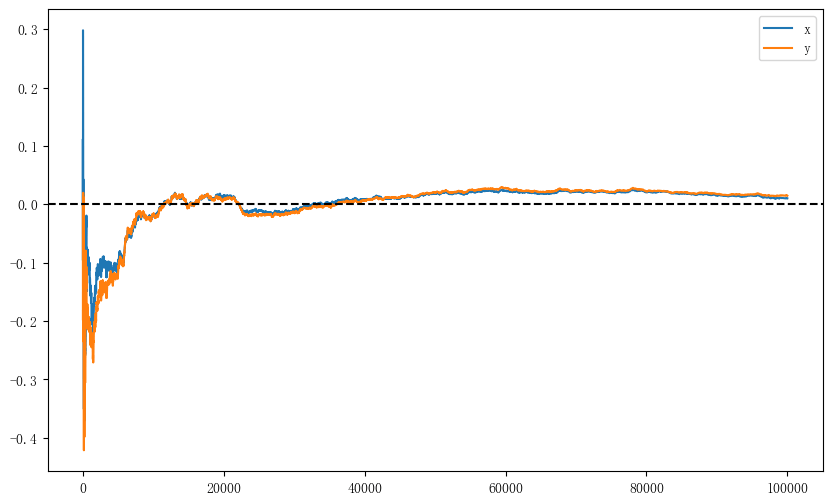
可以看到,当迭代次数达到 50000 时,\(x\)和\(y\)的累计均值都已经趋于一条直线,但还没有非常接近 0。
独立性抽样¶

初始化样本¶
Python
x = 0
y = 0
vector_x_y = np.array([x, y])
# 构造二维独立标准正态分布的理论分布
g = multivariate_normal(mean=np.zeros(2), cov=np.eye(2))
设定迭代次数¶
迭代产生样本¶
Python
for t in tqdm(range(iteration)):
# 生成正态分布随机数
vector_e1_e2_ = np.random.normal(0, 1, 2)
# 将随机数直接赋值到 x 和 y 上
vector_x_y_ = vector_e1_e2_
# 计算接受率
ratio = (two_dimensional_gaussian(vector_x_y_, mu, sigma) * g.pdf(vector_x_y)) / (
two_dimensional_gaussian(vector_x_y, mu, sigma) * g.pdf(vector_x_y_)
)
alpha = min(1, ratio)
# 生成一个随机数 u,它来自均匀分布
u = np.random.uniform(0, 1)
# 如果接受率大于 u,则接受,即更新 x 和 y 的值
if alpha > u:
vector_x_y = vector_x_y_
accept += 1
# 保存样本
# 第一次迭代时,初始化样本
if t == 0:
samples_independent = vector_x_y.copy()
# 后续迭代时,将样本添加到样本集中
else:
samples_independent = np.vstack((samples_independent, vector_x_y))
# 计算接受率
accept_rate = accept / iteration
print("接受率:{:.2%}".format(accept_rate))
Text Only
100%|██████████| 100000/100000 [00:27<00:00, 3602.83it/s]
接受率:58.18%
收敛性诊断——依据各分量的累计均值¶
Text Only
array([[ 0. , 0. ],
[ -0.98714667, -0.81647526],
[ -1.97429335, -1.63295051],
...,
[-380.02483172, -540.44083572],
[-379.2919882 , -540.70237326],
[-380.33205906, -541.43726736]])
Python
fig = plt.figure(figsize=(10, 6))
plt.plot(cummean, label=["x", "y"])
# 绘制辅助线,纵坐标为 0
plt.axhline(0, color="black", linestyle="--")
plt.legend()
plt.show()
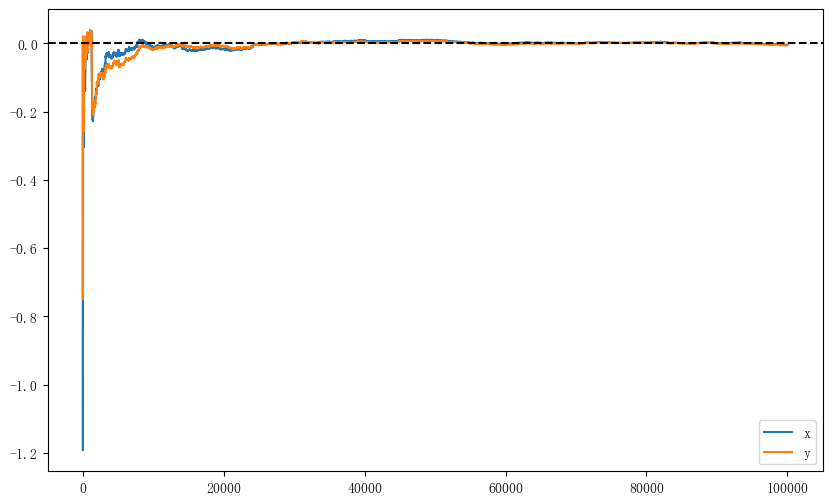
可以看到,当迭代次数达到 30000 时,\(x\)和\(y\)的累计均值都已经趋于 0,说明样本已经收敛。
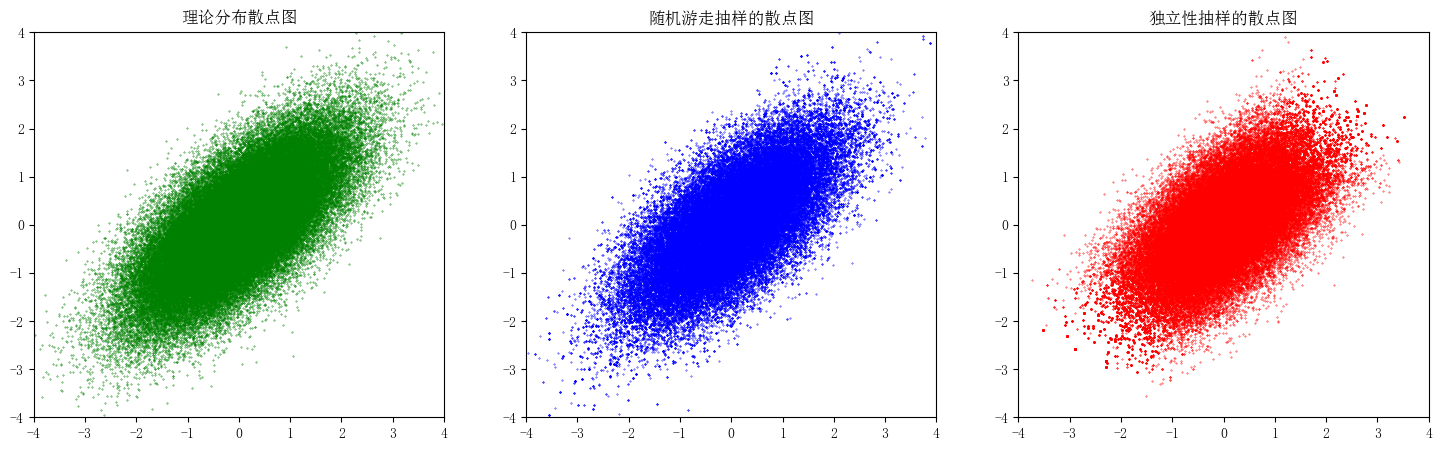
绘制样本的散点图¶
Python
fig = plt.figure(figsize=(18, 5))
# 绘制理论分布的散点图
ax1 = fig.add_subplot(131)
# 生成理论分布的样本
theoretical_sample = var.rvs(100000)
ax1.scatter(theoretical_sample[:, 0], theoretical_sample[:, 1], s=0.1, c="g")
# 标题
ax1.set_title("理论分布散点图")
# 绘制随机游走抽样的样本散点图
ax2 = fig.add_subplot(132)
ax2.scatter(samples_random_walk[:, 0], samples_random_walk[:, 1], s=0.1, c="b")
# 标题
ax2.set_title("随机游走抽样的散点图")
# 绘制独立性抽样的样本散点图
ax3 = fig.add_subplot(133)
ax3.scatter(samples_independent[:, 0], samples_independent[:, 1], s=0.1, c="r")
# 标题
ax3.set_title("独立性抽样的散点图")
# 统一坐标轴范围
for ax in fig.axes:
ax.set_xlim(-4, 4)
ax.set_ylim(-4, 4)
plt.show()

Python
# 将三种抽样的散点图放在一起
fig = plt.figure(figsize=(6, 6))
plt.scatter(
theoretical_sample[:, 0], theoretical_sample[:, 1], s=0.1, c="g", label="理论分布"
)
plt.scatter(
samples_random_walk[:, 0], samples_random_walk[:, 1], s=0.1, c="b", label="随机游走抽样"
)
plt.scatter(
samples_independent[:, 0], samples_independent[:, 1], s=0.1, c="r", label="独立性抽样"
)
plt.legend()
plt.show()
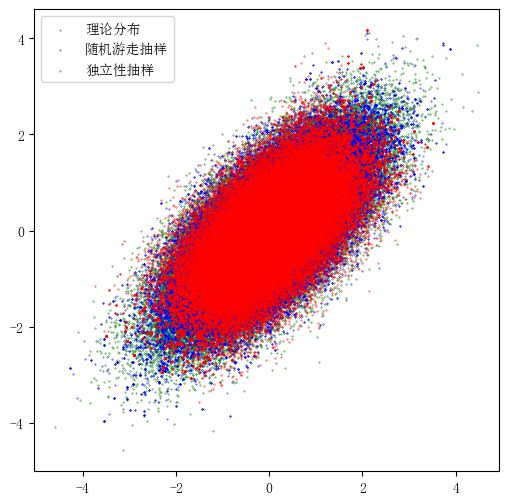
比较两种算法的表现¶
- 随机游走算法的接受率为 45% 左右,独立性抽样的接受率为 55% 左右。
- 随机游走算法的累计均值在前期震荡幅度较大,收敛所需的迭代次数也更多。
- 独立性抽样的累计均值在前期震荡幅度较小,收敛所需的迭代次数也更少,只需迭代 30000 次左右,累计均值就收敛到 0 了。
- 两种算法的样本散点图基本一致,但独立性抽样的样本散点图更加集中,即尾部的样本更少。